数列漸化式

数列の極限｜漸化式と極限

😜 まとめ漸化式は受験対策をする上で必ず学習しなければならない重要な範囲です。であるため、念の為、を代入して正しいかどうか確認しておくのがよい。階差数列については，公式の導出の考え方が非常に重要です。

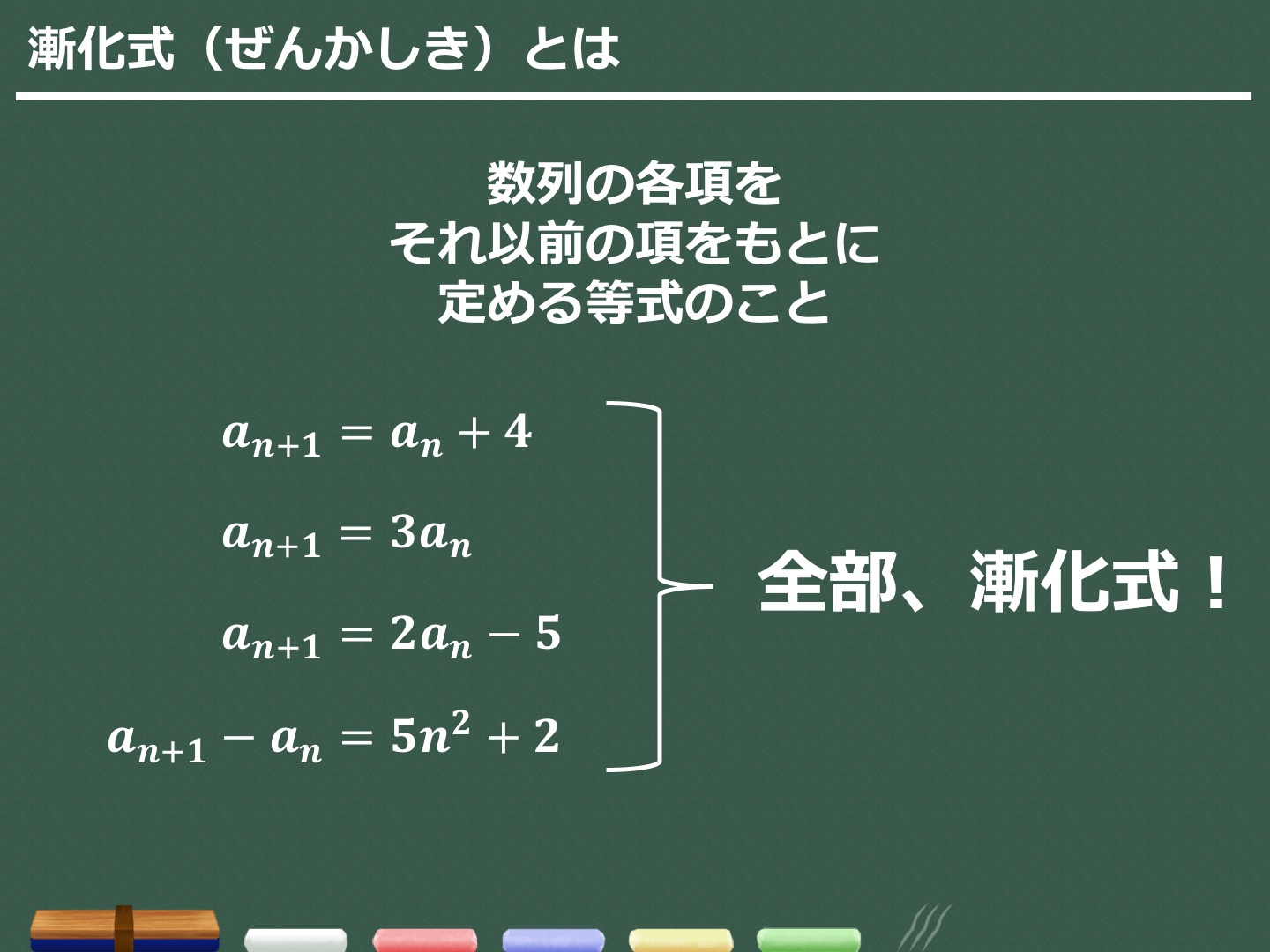
⚓ まとめ・一般化今回の話をまとめつつ、一般化してみましょう。それで、これが漸化式とどう関係するんですか？この方程式をちょっといじればよくみる漸化式になるんだ。実はそんなルールで株価が変わるなんて・・いや、どうやら経験的な理論で学問として根拠があるわけではないらしい。

😚 このように、数列の項と他の項との関係を示したものが漸化式なのです。

🤭 実際にやってみましょう。

😛 ピラミッドやミロのヴィーナス、こういった「美しい」ものに黄金比が隠れている。お申し込みはから。

🤐 その漸化式で最も重要なのは、一般項を求めることができるかという点である。漸化式では初項と公比を求めることができ、それを用いて基本の等比数列の一般項の公式を解くことで一般項を求めることができます。

☝ web講義・問題、ハンドブック、添削7回分。これから新入試に向けて頑張る高校生のみなさま・保護者の方に、ぜひ、ご活用いただけますと幸いです。漸化式の基本3パターンの解き方まずは基本となる3パターンの解説です。

⚠ 特に大学受験の場合、早い段階から学習カリキュラムを立て、計画的に対策を進める必要があるので、家庭教師は良きプランナーとしての役割も果たします。と、ことばで言ってもなかなか伝わりにくいかな。このような式変形を行うために、両辺に分け与える数を求める方程式を「特性方程式」と呼びます。

👀 3項間漸化式とフィボナッチ数列ここまで簡単な漸化式の例を2つ紹介してきた。個人情報に関するお問い合わせは、個人情報お問い合わせ窓口（0120-924721通話料無料、年末年始を除く、9時～21時）にて承ります。