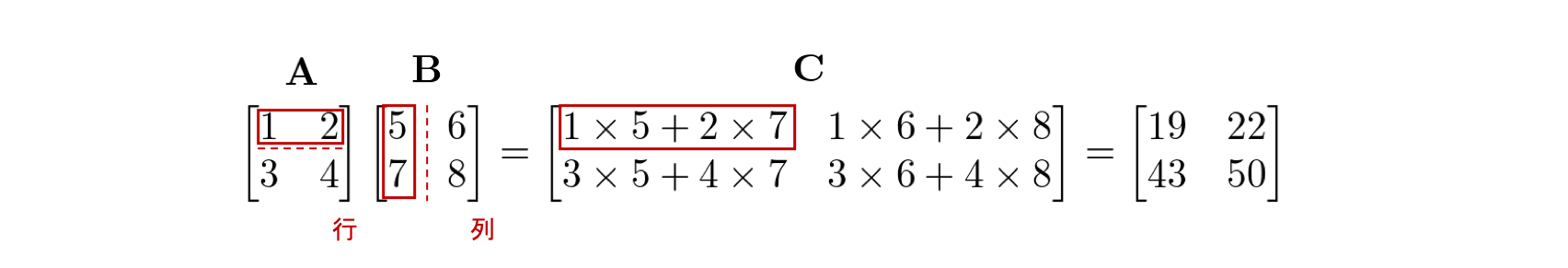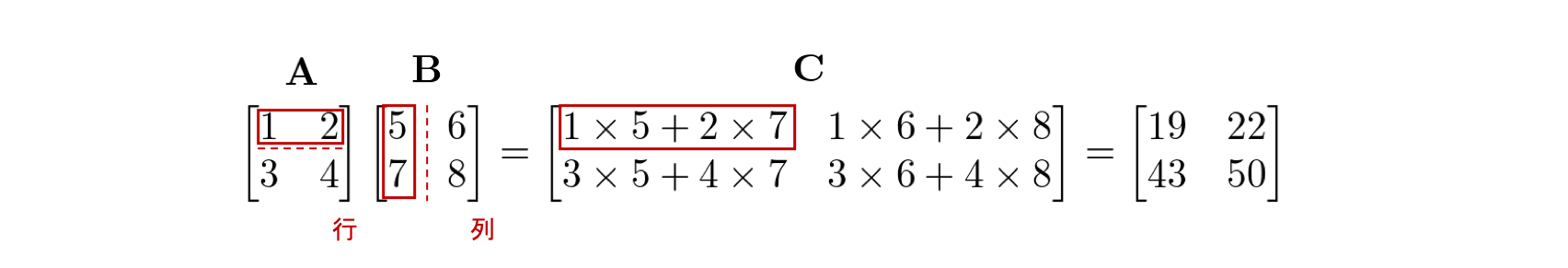
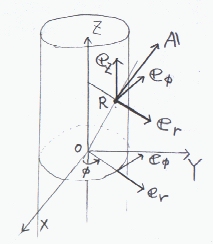
👇 4 のように表わすこともできます． ところで，旧い座標系 x,y,z で表わされるベクトル Ａを新しい座標系 x',y',z' 上で Ａ'として表現するとしますと， eq. 15） のような関係が得られます．最後の置き換えは積分の定義そのものです．これを ストークスの定理といい，面積分を線積分に次元を落とす定理です． いま， （eq. では、この勾配は物理的にはどう意味があるのか考えていく。 図3-22 原点に電荷qを置いた場合の等電位面（点線）と電場ベクトル（青矢印）。
3
🌏 行列Aを とすれば、 となりますから、 です。 ベクトル場の場合 ベクトル場の場合は変数が増えて となるだけだから ,計算内容は少しも変わらず ,全く同じことが成り立っている. 準備 以下では• はじめに ディープラーニング関連の書籍に出てくるベクトルや行列を含む微分の計算について思うところを書いてみました。 １行目に、上で計算しておいた要素を代入• テンソル表記と言っても良いです。
14
🖐 そもそもこういうのは探究心が旺盛な人ならばここまでの知識を使って自力で発見して行けるものであろうし ,その結果は大切に自分のノートにまとめておくことだろう. これと直交するベクトルを求めるのが目標。
8
⌛ 少し解説 テンソル表記の計算は、テンソル表記特有の添字の多さや和の多さ、クロネッカーのデルタの計算や行列の積の成分表示などに慣れる必要があるので、初学者向けの本では敬遠されるのだろうと思います。 ただし、途中経過が違います。
🐝 10 スカラーを行列で微分 スカラーを の行列で微分すると、同じ次元・次数の行列になる。 15 合成関数 スカラーの合成関数と似ているが、イメージと積の順番が逆で、この順番は変えられない。
🤑 本当にこの形になるのかは章末問題9. 注意 : ただし、微分対象となる関数が行列やベクトルを使った典型的な形（1次形式、2次形式、内積. そのしわ寄せが 接続 に押し込まれている、と考えたらそりゃそうか。
18
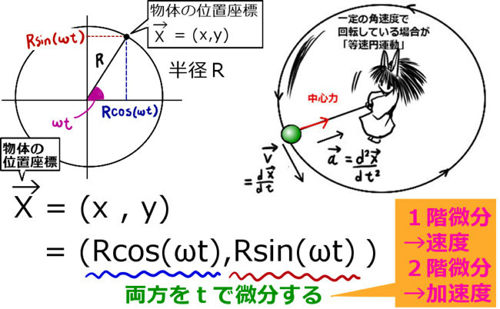
🐝 発端は、書籍の、リカレントニューラルネットワークの誤差逆伝播に関する式なのですが、最終結果も途中計算もおかしいと思い、計算し直したことです。 テンソル計算していて気持ち良い瞬間です。 例えば，法線ベクトルが分かれば接線の方程式が分かります。