標準正規分布表見方

統計学で、zの臨界値を求める時、標準正規分布の表から求める方法を...

🙃 標準を使うデータを用意身長のデータはをする。例として、男子高校生の身長データで話をする。表１のKpからPを求める表に比べるとかなりあっさりしていますね。

♻ この性質を用いたもっと有名なものは、成績を表す偏差値です。

😇 証明正規分布の性質を利用する。

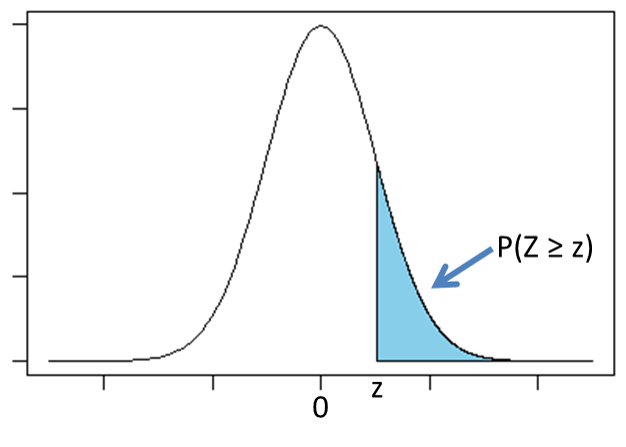
☕ データ部分を選択し、挿入から散布図を選ぶと、平均50で、標準偏差10の正規分布を描くことができました! 今回のような、正規分布表を用いた確率の問題では、等号の有無に左右されずに、どこの面積に、どの確率が表れているか…ということを意識して計算をしていくとよいですね。

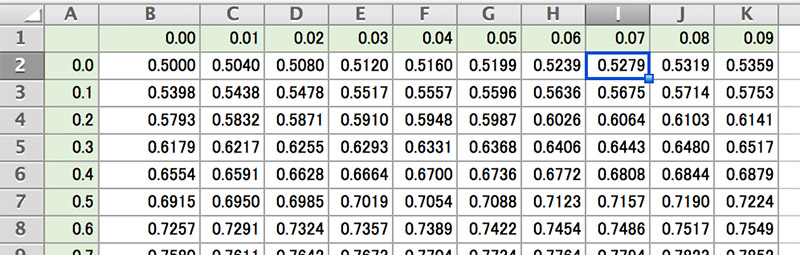
👈 横軸0からある値までの面積であり、それは割合である。また順位で示すとどうなるのか、次の記事で補足説明する。（どちらの表なのか一度使う前にチェックしておきましょう。

☣ もう１問を考えてみましょう。これにより、正規・標準正規分布は推測統計を始めあらゆる分野で利用されることとなりました。 Kenji. 標準表は、「原点の縦軸、横軸、Z値の縦線、曲線」に囲まれた面積が書かれている。

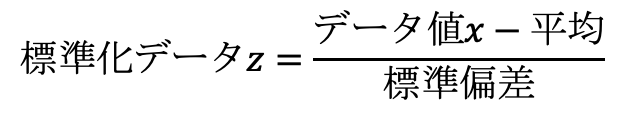
😔 要するに偏差値50というのはちょうど真ん中で、自分より下は2人に1人、自分より上も2人に1人という確率であるということだ。 Zは標準正規分布の確率変数でした。で割っているので、は1になっている。

🤝 まず、整数 1の位＋小数第一位（ここでは1. ところが標準正規分布であればこの面積というのはあらかじめわかっているのです。有意差がなければ学会発表・論文投稿できない• この簡単な操作だけで、どんな正規分布も標準化することができます。）そこで、以下のような正規分布表が与えられます。

😔 なにやら難しい数式ですが、細かい関数の中身は覚えなくてオッケーです！重要なのはグラフの形と、出てくる記号の意味です。