おうぎ形の面積

楕円扇形の面積

🤚 図の色部分の面積を求めなさい。 25㎠例題4 下の図の色の付いた部分の面積を求めなさい。 1 Q、O、Pの順で最初に一直線になるのは何秒後ですか。

📲 A ベストアンサー 1 2 3 は質問者さんの解釈で間違いありません。四角形AQCPの面積が162cm 2になるのはP、Qが同時に出発してから何秒後ですか。画面は、最大画面にするか、フォントを変えるか、メモ帳にＣＯＰＹするかして、図がくずれないようにしてください。

🎇 黄色部分の面積を求める場合、直角三角形の面積を求めるだけでもOKです。・ 4辺の長さと対角の和から四角形の面積を計算します。＊色のついた部分の面積を求めます。

😒 リンク先では半径がわかっていますが、この問題では正方形の一辺の長さがわかっています。円周率は、3. 72㎠正方形とおうぎ形を合わせた形の面積色のついた部分の面積を求めます。

😅 また、図形的に説明はつくと感じていましたが、今日まで、（宿題）になっていました。

🤑 黒くぬった部分の面積を求めなさい。 57」を覚えてしまってもいいです。なお、ひし形や正方形のような、対角線が垂直に交わっている図形は、対角線の長さを用いて面積を求めることができます。

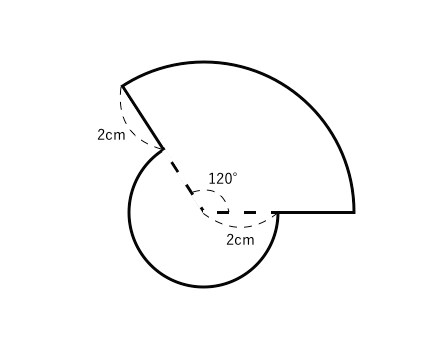
✆ 14とします。

😚 大きい正方形を小さい正方形（1辺５cm） 4つに分けて考えます。必ず０になります。【４ヒポクラテスの三日月（直角二等辺三角形）：三日月の面積＝直角三角形の面積】この「ヒポクラテスの三日月」の形はそのまま出てくる事もよくあります。