トレミーの定理とは

🤔 ありがとうございます。 (コメント) という考え方が、幾何ではいかに素晴らしい考え方かが実感できました! KSさんからトレミーの定理に関する質問です。 すなわち、 よって、 となる。
1
🤔 ありがとうございます。 (コメント) という考え方が、幾何ではいかに素晴らしい考え方かが実感できました! KSさんからトレミーの定理に関する質問です。 すなわち、 よって、 となる。
1
😊 どのような場面において使えるか、具体的な話をすると、 円に四角形が内接しており、さらに対角線が施されていたら、トレミーの定理を使えないかどうか疑ってみる価値があるといえます。 今日は、プトレマイオスの定理の記憶に残る別証明を考えたい。 種々の証明を見ても対辺の積を足し合わせることの幾 何学的意味がどうにも納得できず長年もやもやしていたのですが、先ほどそれを納得できる 証明をふと思いつきました。
10
😊 発想と思いつきがそれなりのウエイトを占める図形問題において、トレミーの定理を使うことで予期しない突破口が開けることは多々ありますよ。 円に内接する四角形の各辺と、2本の対角線をあわせた6本の辺があります。 S(H)さんが考察されました。

♨ 対角線の数=7C2=21本である。 (追々記) 最近、 の応用題で、トレミーの不等式なるものを用いた。
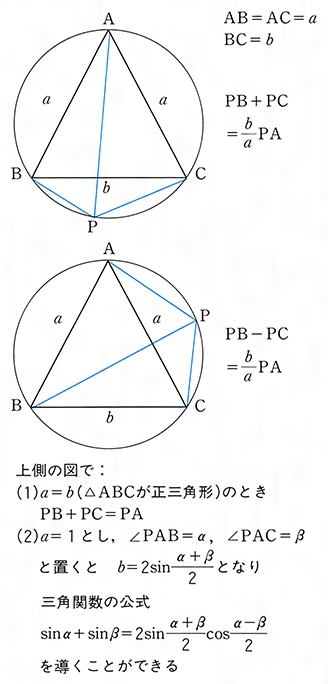
☎ 円に内接する四角形において、 対角線の積は対辺の積の和に等しい。 基礎・基本を重視し ているのは感じとれるが、さらに突っ込んだ話の展開が削除されているので、ちょっと実力を 身に付けるのは厳しいな、というのが率直な感想である。 このように、一つのプトレマイオスの定理から、幾何学的に重要なピタゴラスの定理、三角 関数の加法定理が導けるということは、非常に驚くべきことである! (参考文献:エリ・マオール 著 好田順治 訳 素晴らしい三角法の世界(青土社)) (追記) プトレマイオスの定理の上記の証明は、とても強引すぎて、鮮やかだけれども美し さは感じられない。
19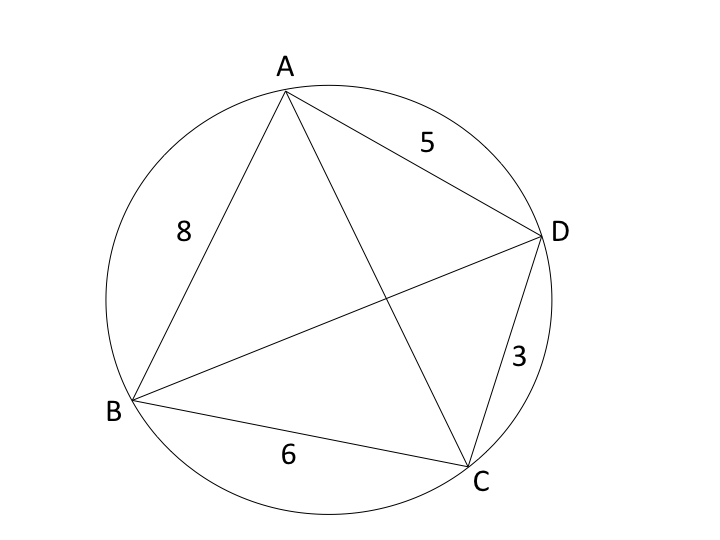
💋 新しい定理を覚えるととりあえず使ってしまいたくなる気持ちはわかるのですが、高校数学は知識のひけらかし大会ではありません。