数列の和

🤝 しかし毎回このように考えていると時間がかかってしまいます。 等差数列は、「１，３，５，７，９」のように、となり合う２つの数字の差の大きさが一定の数列です。 ここでのポイントは次の2つです• 同じ「3, 6, 12, 24, 48. ここでは，その和について考えてみることにしましょう。

15

【等差数列の和と等比数列の和】小学生が解く！中学受験の算数

☭ 要するに S 10 を求めればよいわけですから，少し技巧的ですが， 1 と 2 辺々 左辺は左辺，右辺は右辺 加え合わせますと， となります。

14

等比数列の和と等比級数

💅 等比数列の和の応用例 最後に，等比数列の和の公式の考え方を使ったいろいろな応用例を紹介します。

数列の基本７｜[等差×等比]型の数列の和は引き算がポイント

😅 またそれぞれの数にかける数を公比と言います。

15

等比×等差の和を求める２通りの方法

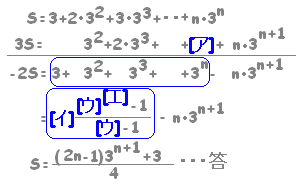
😜 ですので、元の式を3倍してずらして引く方法を使います。 ここで、xSn-Snを考えてみると、 ものすごくごちゃごちゃしていますが、「…」なしにSnを求めることができました。

13

等比数列の一般項と和

🐾 下の図を見てください。 この時の 「差」のことを「公差」と言います。 文字で公式を覚えようとすると、文字を覚え間違っていたり、間違った数値を入れてしまったり、自分が何をしているのかわからなくなったりしますが、 日本語で覚えると、そういった心配があまりないのでおすすめです！ 和の公式が出てくる問題で練習しよう ここでは、実際に和の公式を使って問題を解いてみましょう。

【等比数列まとめ】和の公式の証明や一般項の求め方を解説！応用問題つき

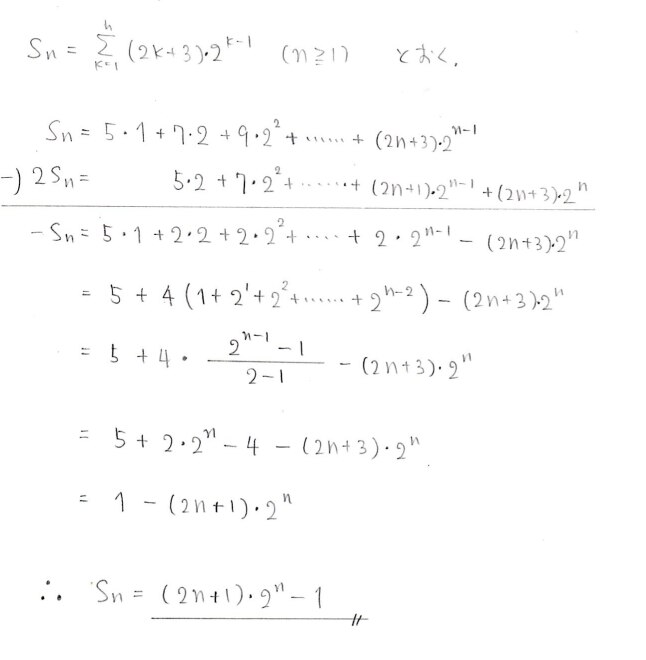
😔 数列の和の計算では、rを掛ける等の変形で、既に公式が分かっている形に変形する。 そうすると赤枠の部分は0になるので消えて、4374-2で4372が残ります。

【等差数列の和と等比数列の和】小学生が解く！中学受験の算数

😎 2 式で求まる。 エクセルを用いた等差数列・等比数列の和 連続試合安打の継続数は無限等比級数 エクセルを用いた等差数列・等比数列の和 連続試合安打の継続数は無限等比級数 Excelを用いた科学技術計算が第2版になりました 30年10月 ！ amazon： 楽天： 図 連続試合安打の継続数は無限等比級数 等差数列 1,3,5,7,9,11,・・・ のように隣り合う項の差 公差 が等しい数列を等差数列という。 この単元では、規則性の把握が求められます。

9

等比数列の一般項と和

👏 ですので、次にくる数値は256だと予測できます。 「初項」「公比」だけを押さえれば一般項は求められる いま、等比数列とは「初項にある一定の数をかけ続けていった数列」といいました。 あとは，両辺を 1-r で割り，S n を求めればよい，と言いたいところですが…。