ラグランジュの運動方程式とは
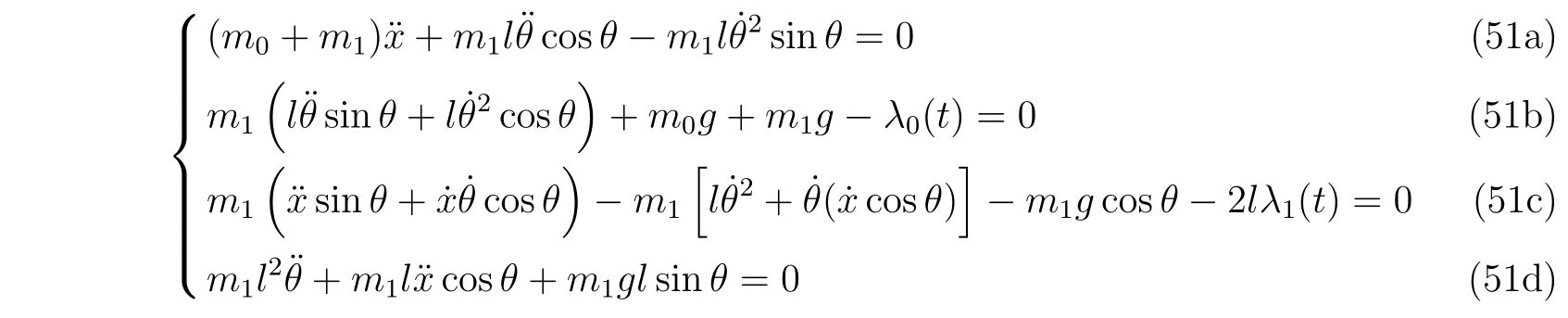
☣ だから 慣性系に固定された座標系では、運動エネルギーとしてどの慣性系での運動エネルギーを採用しようとも時間を含まない。 一般座標でのラグランジュ方程式 さて準備ができたので一般座標でのラグランジュ方程式というものを説明しよう。 ということは、ニュートンの運動方程式 1 と等価な 7 の後ろには、変分法的な何かが隠れていそうだ。
4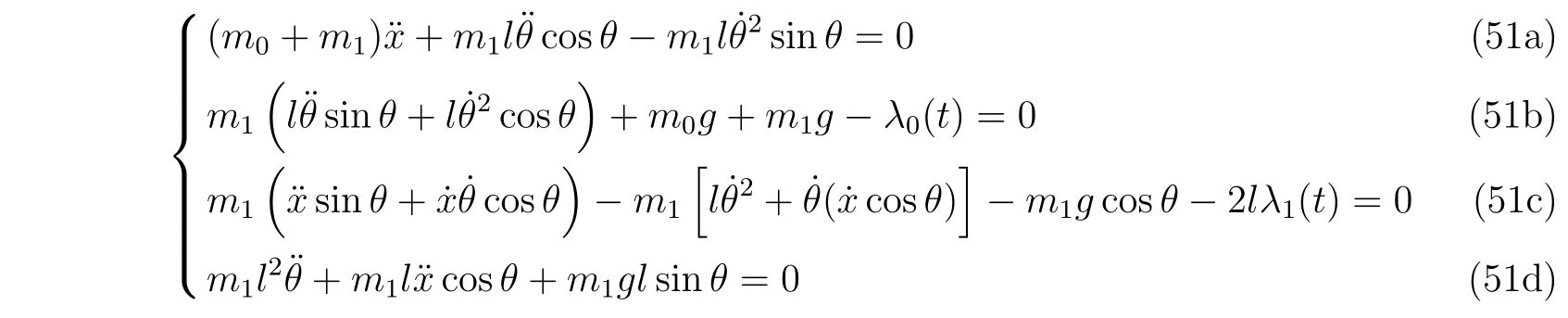
☣ だから 慣性系に固定された座標系では、運動エネルギーとしてどの慣性系での運動エネルギーを採用しようとも時間を含まない。 一般座標でのラグランジュ方程式 さて準備ができたので一般座標でのラグランジュ方程式というものを説明しよう。 ということは、ニュートンの運動方程式 1 と等価な 7 の後ろには、変分法的な何かが隠れていそうだ。
4
👇 この関係式を用いて運動方程式を求めていきます。 それを今から述べていく。 ニュートンの運動方程式からラグランジュの運動方程式へ さて必要な公式が整ったところで、ニュートンの運動方程式をラグランジュの運動方程式に一気に持ってゆきましょう。
20
⚐ おっしゃる通り、ラグランジュの方法はシステマチックで、淡々と進めれば運動方程式が出てきます。 だから 慣性系の直交座標では、運動エネルギーとしてどの慣性系での運動エネルギーを採用しようとも時間を含まない。
12😁 個のホロノーム型 後述 束縛条件が存在すると、自由度は 個に減少します。
😆 しかし、解析力学では、束縛力を直接扱わずに式を立てられるため、運動方程式が非常に単純化されます。 上でも触れたとおり、ラグランジアンや作用を適切に定義することにより、 ニュートン方程式だけでなくマクスウェル方程式や一般相対論などについても 最小作用の形で定式化できることが知られている。 ただもし「極小値」であったとしてもそれが真の「最小値」であるのか、についてはここまでの議論からは判然としない。
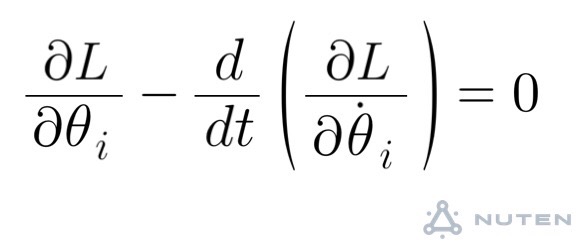
🤚 ばねはフックの法則に従い、摩擦はないものとする。 そのため、運動方程式は非線形な関数になっています。 つまり、仮想変位 は3N次元空間の超曲面 に垂直な多次元ベクトル成分を含みませんから、質点に加わる力のうち、超曲面 に垂直な方向 広義の法線ベクトル を基底とする部分空間のベクトル方向の力は仕事をしません。
1