内接円の半径

【三角比】内接円の半径の求め方をイチから丁寧にやってみよう！

😔 これをrについて解けば答えがでます。弧 AB に対する円周角は点 P の位置に依らず一定であり、中心角 AOB の半分に等しい（円周角の定理）。三角形の内部にある円の中で最も面積が大きい円である。

三角形の内接円と傍接円の半径に関する性質

✔ 三角形の1辺の長さとその対角がわかっていたら？まずは 1辺と対角のセットがないか探します。

【3分で分かる！】三角形の外接円の半径の長さの求め方をわかりやすく

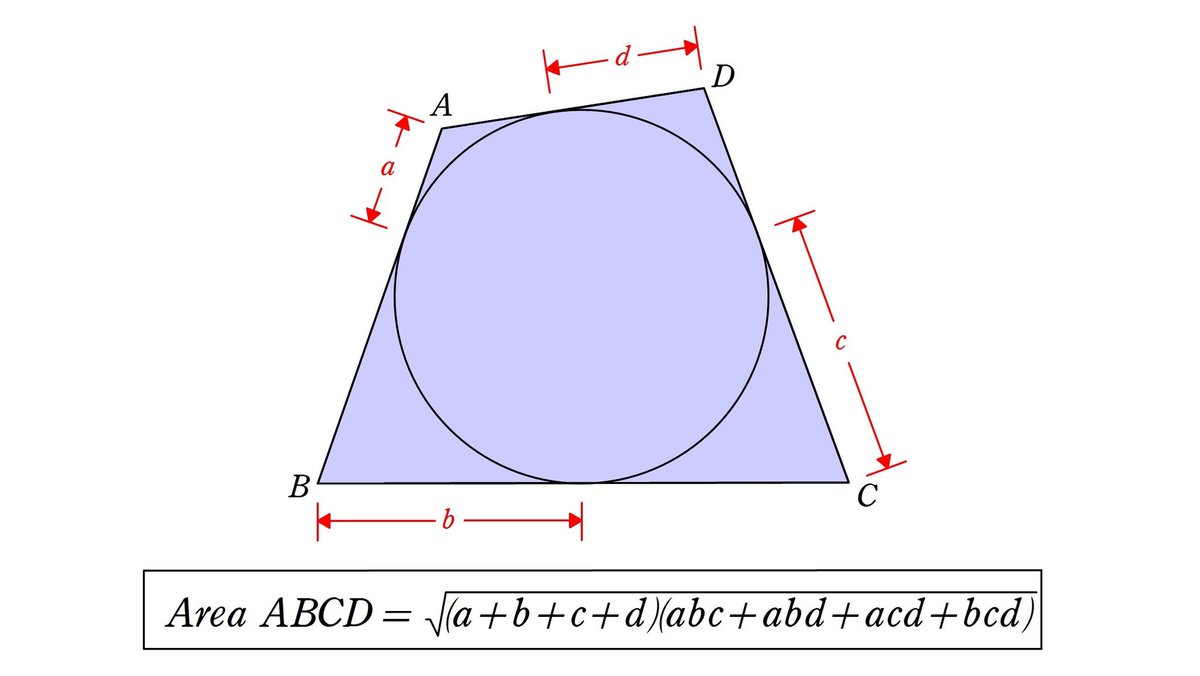
🙃 よって、この幾何学で（半径に対する周長の比）に相当するものは 4 ということになる。

【3分で分かる！】三角形の内接円の半径の長さの求め方（公式）をわかりやすく

😄 この形（ x 2, y 2 の係数が等しく、 xy の項を持たない）の方程式が与えられたとき、以下の何れか一つのみが成り立つ:• - 内接円の接線と面積に関する定理外部リンク [ ]• このとき、割線は円の中心を通る中心線である。これでは優弧・劣弧のどちらであるかを指定できていないデメリットがあり、一方を特定したい場合は、その弧上の点 P を用いて弧APB のように表記する。答えは、およそ36. 三角形のなかに1つの円がすっぽりはまっている図をイメージするとよいでしょう。

接円

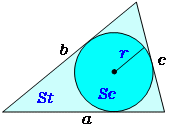
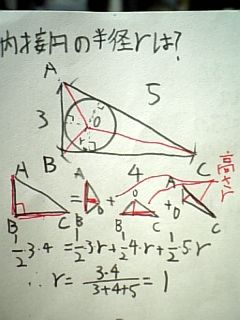
🤞 の外接円• ３．接円の中心を指示します。円の半径ｒとし、ABにOから下ろした垂線の足をLとすると、AB＝ａ＋ｂならば、ABは円に接するすなわち OL＝ｒであることを証明すればよい。円 A が円 B の周または内部にあり、1点のみを共有する場合 : 円 A は円 B に内接するという。

内接円の半径と三角形の面積

🤟 まずは，多くの参考書に載っている有名な証明方法です。 2つの弧の長さが等しくないとき、長い方の弧を優弧 major arc 、短い方の弧を劣弧 minor arc という。

高校数学A【図形の性質】内接円と接線まとめと問題

$接の半径円内$

😍 Pから、AB,ACへ下ろした垂線の足を、それぞれD,Eとします。共通外接線2本• 問題下の図のような三角形に内接する円の半径を求めなさい。